· 잔차 분석
가로축이 yhat, 세로축이 잔차로 그래프를 통해 쉽게 알아볼 수 있다.
잔차 e_i = y_i - yhat_i는 회귀식을 적합시키고 남은 것으로, 설명변수로는 전부 설명할 수 없는 영향(력)이 남아 있다.
이 잔차는 직선 모형이 적합했는지, 오차항에 대한 가정들은 타당했는가를 확인할 수 있는 방법 중 하나이다.
한 편, 잔차는 오차항의 관측값을 볼 수도 있다. (즉, εhat_i = e_i)
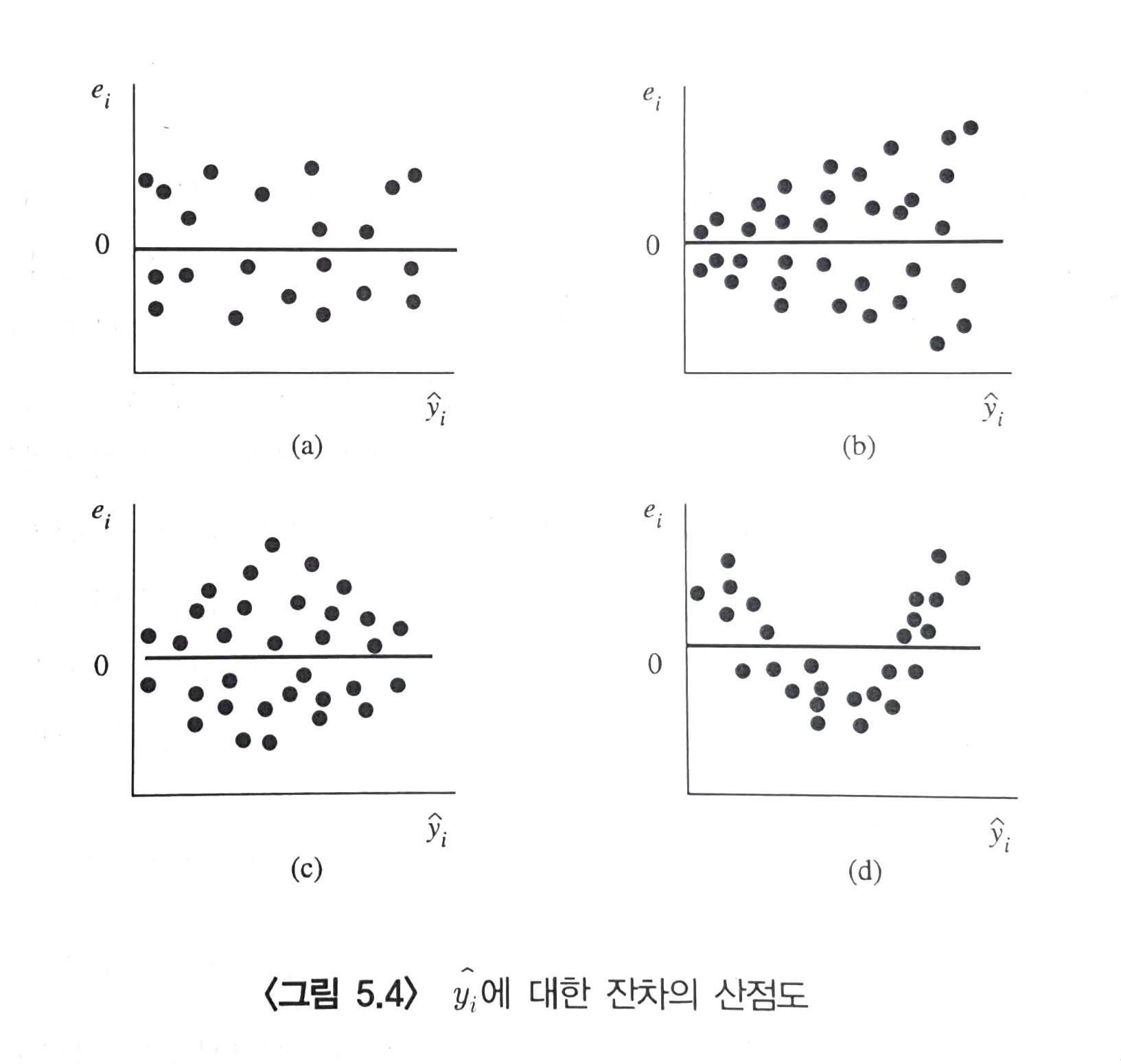
· 회귀 함수의 선형성(모형 적합성)
(1) 설명변수와 반응변수 사이에 선형적인 관계가 타당한지 확인
(2) 잔차 그래프(평균 반응값과 잔차), 산점도의 모양으로 판단할 수 있다.
(3) 회귀분석 전 두 변순들이 산점도에서 선형 관계가 적절하다면, 잔차 그래프가 어떤 패턴이나 특정 형태 없이 중심으로 잡는 0을 기준으로 랜덤 하게 배치된 모양이어야 한다.
(4) 만일 곡선의 모양 또는 특정한 패턴이 나타나면, 선형이 아닌 다소 복잡한 모형을 사용하여 자료를 분석해야 한다.

(a) 가장 바람직한 모습이다.
(b) 이차곡선에 적합한 모습이다.
(c) 삼차곡선 또는 sin, cos 곡선에 적합하다.
(d)와 (e)는 비정상적인 모습임을 단번에 알 수 있다.
· 오차항의 등분산성
n개의 오차항이 모두 같은 분산을 갖는 분포로부터 추출되었는지 확인한다.
특정 설명변수 구간에서 뚜렷하게 크거나 작으면 등분산 가정에 타당하지 않다고 판단할 수 있다.
(a) 바람직한 잔차의 분포(랜덤 하게 퍼져있다.)
(b) 반응 변수 값이 클수록 오차의 분산이 증가한다.
(c) 반응변수 값에 따라 오차 분산이 증가하다가 감소하는 추세
(d) 이차함수의 모양을 띄는 형태
· 오차항의 독립성 검정
오차항들이 서로 독립적인 관계를 갖는지 확인하는 과정이다.
잔차의 합은 언제나 '0'이므로 원칙적으로는 잔차들은 서로 독립이 아니다. 하지만 자료의 쌍의 수가 어느 정도 크게 되면 독립성 검정에 별 다른 영향이 없다고 판단할 수 있게 된다. (대략 10개 정도)
마찬가지로 잔차의 그림에서 규칙성(패턴)이 보이면 독립성을 의심한다.
크게 독립성이 의심된다면 DW 검정을 실시한다.
특히 독립변수(또는 설명변수 x)가 시간을 나타낼 경우에는 Durbin-Waston 검정을 반드시 실시하는 것을 권장한다.
오차가 이전 오차값에 영향을 받는지도 검정해야 한다.(자기 상관관계)
(a) 가장 바람직한 모형이며 그 외의 모형들은 다른 모형을 적용하거나 문제가 있는 형태이다.
- 오차가 이전 오차값에 영향을 받는지를 검정하는 자기 상관에 대한 검정 방법(독립성)
<Durbin - Waston 검정>

R에서는 lmtest라는 패키지를 다운로드하여서 실행할 수 있다.
· 오차항의 정규성 검정
오차항들이 정규분포로부터 추출된 것이 맞는지 검토한다. 이는 잔차를 이용해서 판단할 수 있다.
오차들의 분포 모양을 살피는 방법으로는 잔차의 histogram을 그려보거나 정규 qq-plot을 그려본다.
여기서 종 모양의 대칭형 hist인지, qq-plot은 45 º 각도의 직선에 가까운 점들이 그려지는지 확인한다.
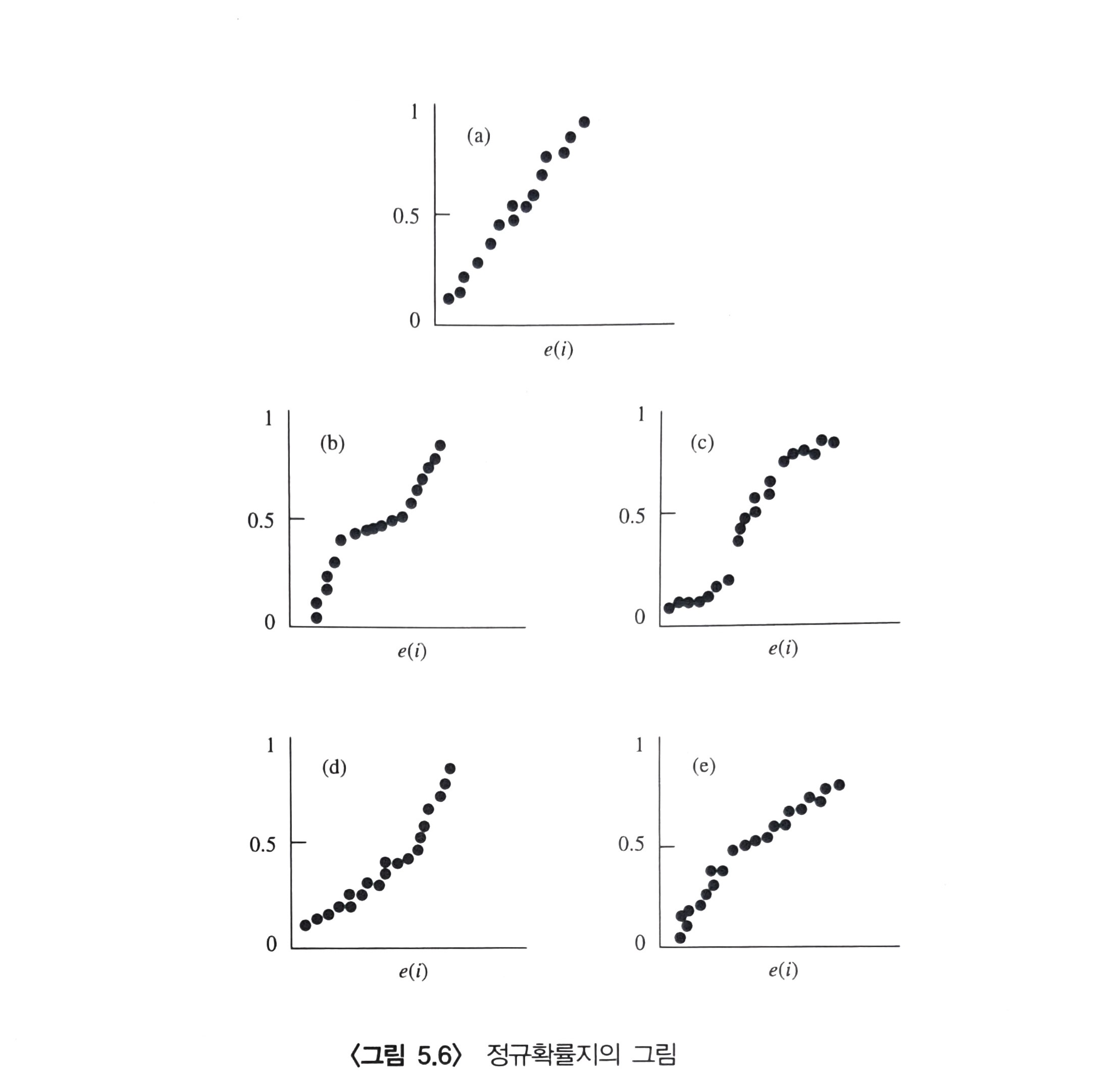
<Shapiro-Wilk 검정>
가설 - 귀무 가설 : 자료가 정규분포를 따른다. vs 대립 가설 : 자료가 정규분포를 따르지 않는다.
<예제>
x = c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10) # 가열시간(분)
y = c(170, 106, 92, 80, 69, 47, 45, 30, 28, 18) # 박테리아의 수
datas = data.frame(x, y)
result = lm(y ~ x, data = datas)
result # yhat = 146.87 - 14.25 * x
yhat = 146.87 - 14.25 * x
res = residuals(result)
# 분포를 통한 선형, 등분산 확인
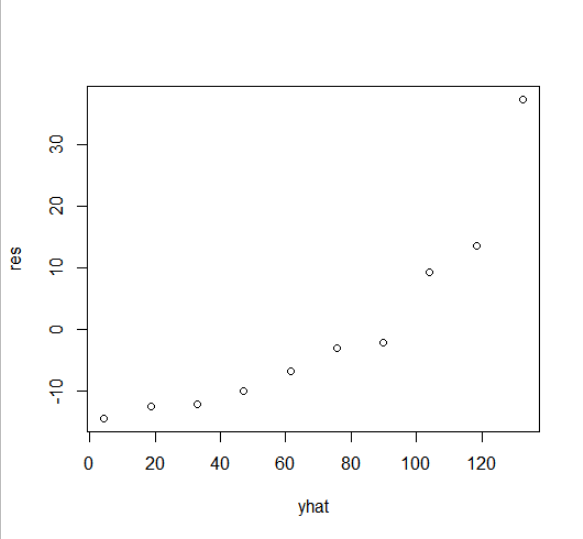
plot(yhat, res) # 잔차 그림
abline(h=0, col="red")
# 선형성 확인
library(car) # 다공선성 및 선형성을 확인하기 위한 패키지
boxTidwell(y ~ x, data = datas) # 8.818e-06 ***, 귀무가설 기각 선형이 아니다.
# 등분산성
ncvTest(result) # p = 0.042109, 귀무가설 기각, 등분산성을 만족하지 않는다.
# 독립성
library(lmtest) # dwtest를 사용하기 위함
dwtest(y ~ x, data = datas) # DW = 1.2309, p-value = 0.03459, 독립이라고 보기 어렵다.
# 정규성
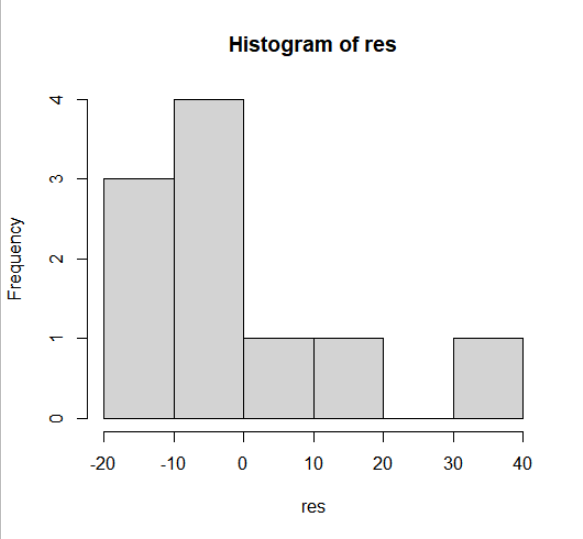
hist(res) # 잔차의 히스토그램 : 종 모양이이라고 보기는 애매하다.
qqplot(yhat, res) # 정규 분위수 그림, 45도로 완벽하게 우 상향을 하진 않는다.
shapiro.test(res) # p-value = 0.03215, 귀무가설 기각 - 정규성을 만족하지 않는다.
newdt = data.frame(x = c(11, 12, 13)) # 11분 ~ 13분까지 알고 싶은 데이터를 추가
pred = predict(result, newdata = newdt, interval = "confidence") # 신뢰구간을 포함하여 예측
pred = predict(result, newdata = newdt, interval = "prediction") # 예측구간을 포함하여 예측
pred
<plot(yhat, res)의 결과>

<hist(res)>
<qqplot(yhat, res)>
'통계 > 회귀분석 - R 프로그래밍' 카테고리의 다른 글
| 회귀분석 - 중회귀모형 (4) | 2021.06.24 |
|---|---|
| 회귀분석 - 원점을 지나는 회귀 (0) | 2021.06.23 |
| 회귀분석 - 결정계수 + 분산분표(R) (0) | 2021.06.21 |
| 회귀분석 - 분산분석 (2) | 2021.06.21 |
| 평균반응량 E[y] = μ(y, x)의 신뢰구간 (0) | 2021.06.20 |