· 중회귀 모형의 분산분석
중회귀에서도 단순 회귀와 같이 분산분석을 통해 회귀의 유용성(타당성)을 검증할 수 있다.
단순 회귀에서의 분산분석의 경우 가설은 아래와 같다.
(가설)
귀무가설 : β1 = 0 vs 대립가설 : β1 ≠ 0
종합하면 회귀식은 무의미하다 vs 회귀식은 유의하다. 정도로 나타낼 수 있었다.
하지만, 중회귀에서의 분산분석의 경우 매우 강력한 가설을 갖고 있다.
(가설)
귀무가설 : β1 = β2 = β3 =... = βi = 0 vs 대립가설 : β1 = β2 = β3 =... = βi ≠ 0
요약하면 절편을 제외한 모든 회귀계수들이 0이다. vs 적어도 하나 이상의 회귀식은 유의미하다.
검증 결과 대립가설이 채택되었다면, k 개의 설명변수 중 적어도 하나의 변수가 반응변수와 선형 관계를 갖고 있다는 것을 의미한다.
· 중회귀의 분산 분석표
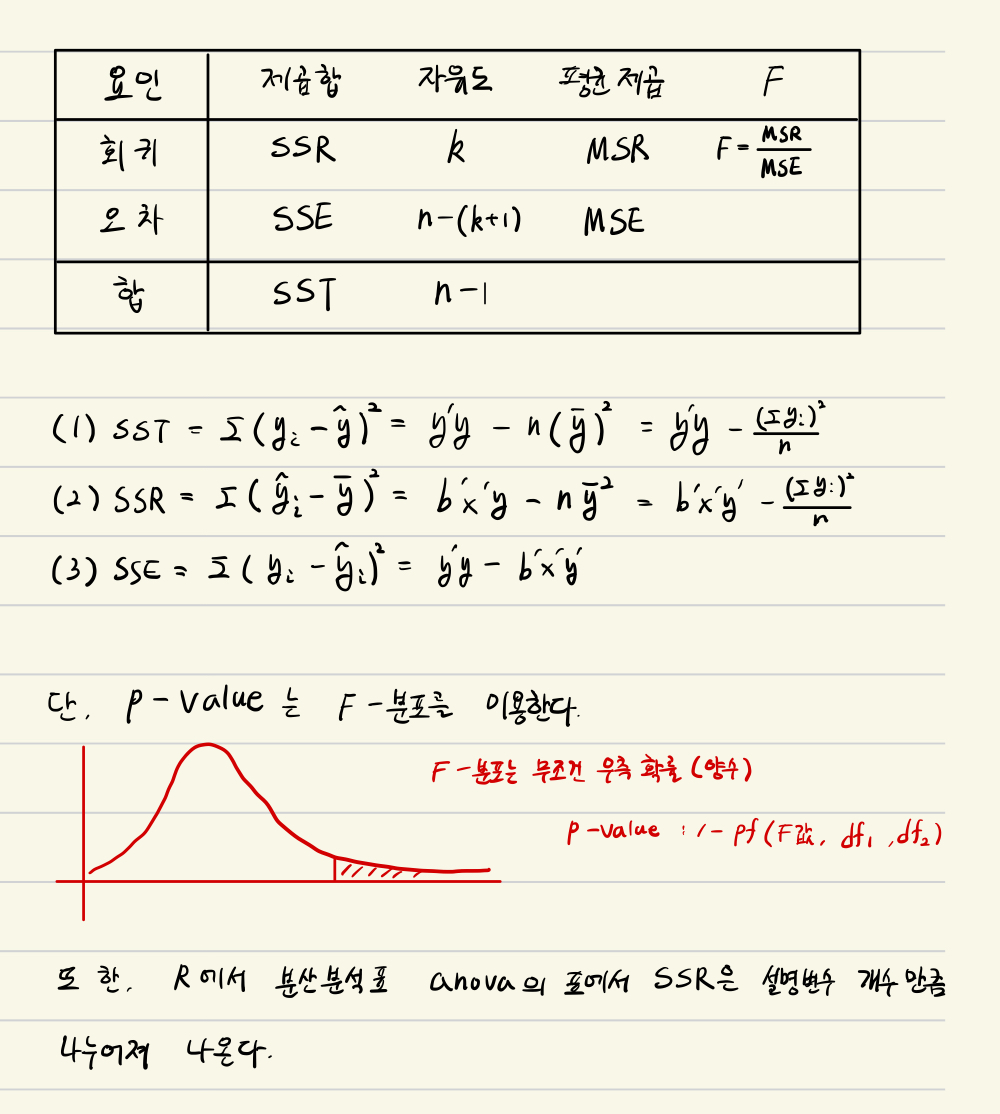
· 중회귀 모형의 타당성
자료에 대한 모형이 적절한지에 대한 것은 추정한 회귀 식이 얼마나 자료를 잘 설명하는가에 대해 매우 중요한 것이다.
주어진 값을 잘 계산해도 모형이 적합하지 않는다면 분석 결과는 아무런 쓸모가 없는 숫자일 뿐이며 잘못된 결과로 결론을 내릴 수도 있기 때문이다.
· 결정계수
중회귀 모형의 결정계수의 식은 단순 회귀 모형과 동일하다.
(결정계수 공식)
R = (SSR / SST) = (1 - SSE / SST)
결정계수의 수가 1에 가까울수록 회귀 식이 자료에 더욱 적합하다고 볼 수 있으나, 이 값이 큰 것이 무조건 좋은 회귀 결과라는 것은 아니란 점을 꼭 명심해야 한다. 단지 간단하게 살펴볼 수 있는 값 중 하나다.
왜냐하면 중회귀에서는 독립변수를 추가할 때마다 실제 종속변수에 영향을 주지 않을 때에도 결정계수는 증가하기 때문이다.
이는 수정된 결정계수를 참고하는 것이 좋으나 모형의 결정 등에는 결정계수 외의 기준을 먼저 살펴본 후 최적의 모형을 결정하는 것이 좋다.
· 잔차 분석
단순선형 회귀에서도 잔차 ei = yi - yhat_i를 분석하는 것이 모형의 적합성을 알아보는데 중요하다고 했었다.
2021.06.22 - [통계/회귀분석 - R 프로그래밍] - 회귀분석 - 모형진단(오차항, 잔차 분석) + R예제
잔차에 대한 분석은 가장 먼저 잔차 그림을 통해 이루어진다.
모형의 적합성 : plot 그림을 통해 빠르게 판단
오차항의 등분산성 : 잔차 그림과 분포도로 판단하거나 nvcTest(회귀분석한 변수)을 통해 알아본다.
오차항의 독립성 : 더빈 왓슨으로 판별
오차항의 정규성 : hist그림, qq-plot, shapiro.test()를 통해 결과를 종합 후 나열한다.
· 절편이 없는(원점을 지나는) 중회귀 모형

위 식을 vector와 행렬로 표현하면, y = xβ + ε으로 일반적인 회귀와 동일하게 보이나,
Design 행렬에서 첫째 열의 1 vector가 없으며 회귀계수 vector에도 β0도 없다.
회귀계수는 절편이 0이 아닌 일반 중회귀 모형의 회귀계수와 일치한다.

· 원점을 지나는 중회귀 모형의 분산 분석
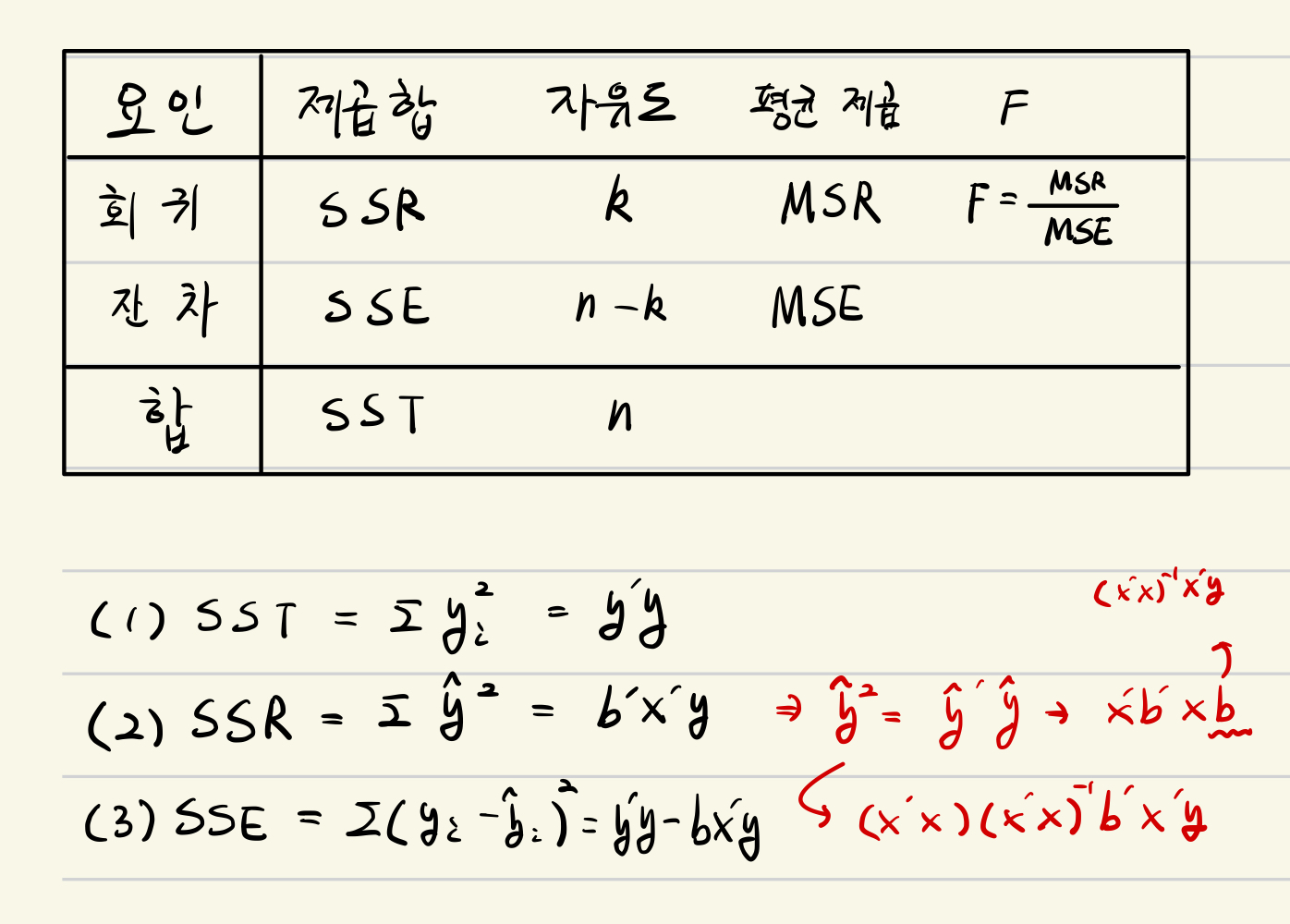
<예제>
# 중회귀 모형의 비교
x1 = c(2, 2, 4, 2, 2, 4)
x2 = c(1, 1, 1, -1, -1, -1)
x3 = c(0, -1, 1, 0, -1, -1)
y = c(14, 17, 18, 12, 14, 16)
df = data.frame(x1,x2,x3,y)
# 일반 중회귀 모형을 가정하고 회귀 실시
reg = lm(y ~ x1 + x2 + x3)
reg # 10.286 + 1.679 * x1 + 1.571 * x2 - 1.214 * x3
yhat = 10.286 + 1.679 * x1 + 1.571 * x2 - 1.214 * x3
summary(reg) # 0.1016, 0.1136, 0.2771 > 0.05 : 설명변수들의 값들이 전부 p-value보다 크므로 귀무가설 기각 불가.
# 독립변수들은 귀무가설을 기각할 수 없으므로 (기울기가 0이다.)
# 반응변수는 0.0275 * < 0.05 이므로 귀무가설을 기각한다. 하지만 비교를 위해 원점 중회귀를 실시해본다.
# 전체적인 p-value: 0.1837 > 0.05 귀무가설을 기각할 수 없다. 해당 회귀에 대해 의심을 가져야 한다.
# 분산 분석
anova(reg) # 0.1269, 0.1502, 0.2771 > 0.05 : 설명변수 모두 유의수준 값 보다 크므로 귀무가설을 기각할 수 없다.
# 그렇다는 것은 모든 설명변수의 회귀 계수는 0이라는 뜻이다.
par(mar = c(2,2,2,2))
par(mfrow = c(2,2))
plot(reg)
# 원점을 지나는 회귀 실시
reg2 = lm(y ~ 0 + x1 + x2 + x3)
reg2 # 4.917 * x1 + 2.333 * x2 - 3.5 * x3
yhat2 = 4.917 * x1 + 2.333 * x2 - 3.5 * x3
summary(reg2) # x1 : 0.00521 ** < 0.05 귀무가설 기각 기울기는 0이 아니다.
# 전체적인 p-value: 0.01406 < 0.05 이므로 귀무가설 기각 => 유의미하다고 볼 수 있다.
# 분산 분석
anova(reg2) # x1 : 0.003786 ** 귀무가설을 기각한다. x1의 회귀계수는 0이 아니다. x1만이 유의미하다는 것이다.
par(mar = c(2,2,2,2))
par(mfrow = c(2,2))
plot(reg2)
# 추가적으로 추가 제곱합에 대한 계산을 구하자면 다음 예시를 보자.
# R(β2 | β0, β1, β3)에 대한 추가 제곱합을 구하고, 95%에 대한 유의수준 검사를 해라.
reg3 = lm(y ~ x1 + x3 + x2) # 위 식은 절편, x1, x3에 데이터에 x2를 추가했을 때 제곱합을 구하라는 것이다.
anova(reg3) # 위 식에 x2에 대한 추가 제곱합은 11.5238이다.
# 0.1136 > 0.05 이므로 귀무가설을 기각할 수 없다. x2의 회귀계수는 0이다. 기울기로써 작동하지 못한다.


'통계 > 회귀분석 - R 프로그래밍' 카테고리의 다른 글
| 변수 선택 방법(AIC) (0) | 2021.06.30 |
|---|---|
| 중회귀모형 - 다(중)공선성, 분산팽창 인자(VIF), 상태지수(CI) (0) | 2021.06.28 |
| 중회귀모형 추론(추정)과 검정 + R예제 (0) | 2021.06.25 |
| 중회귀분석 - 추정량들의 특성 (0) | 2021.06.25 |
| 회귀분석 - 중회귀모형 (4) | 2021.06.24 |