728x90
반응형
· 단순 회귀 모형
단순 회귀 모형은 연속성을 가지는 두 변수 x와 y가 쌍(Paired)을 이루는 형태를 가정하고 시작한다.
여기서 연속성이란, 범주형 데이터가 아닌 연속형 데이터를 의미한다.
· 자료의 모양
(x1, y1), (x2, y2), (x3, y3), ..... , (xn, yn)의 모습을 하고 있다.
x 데이터 집합과 y 데이터 집합 간의 상관관계가 있다고 판단되면 해당 직선 관계에 대해 요약할 수 있는 직선의 식을 찾을 수 있다.
영향을 주는 변수 x를 독립변수(설명변수), 영향을 받는 변수 y를 반응변수(종속변수)라고 한다.
· 단순 선형 회귀 모형
두 변수 사이의 직선 관계는 다음의 식과 같이 표현할 수 있다.
모형 : yi = β1 * xi + β0 + εi (단, i = 1, 2, 3, 4, ... , n)
yi = i 번째 종속 변수
xi = i 번째 독립 변수
β1 = 직선의 기울기(slope)
β0 = y의 절편(intercept)
εi = 오차항(error)
· 단순 선형 회귀 모형에서의 오차항(ε)에 대한 가설과 성질
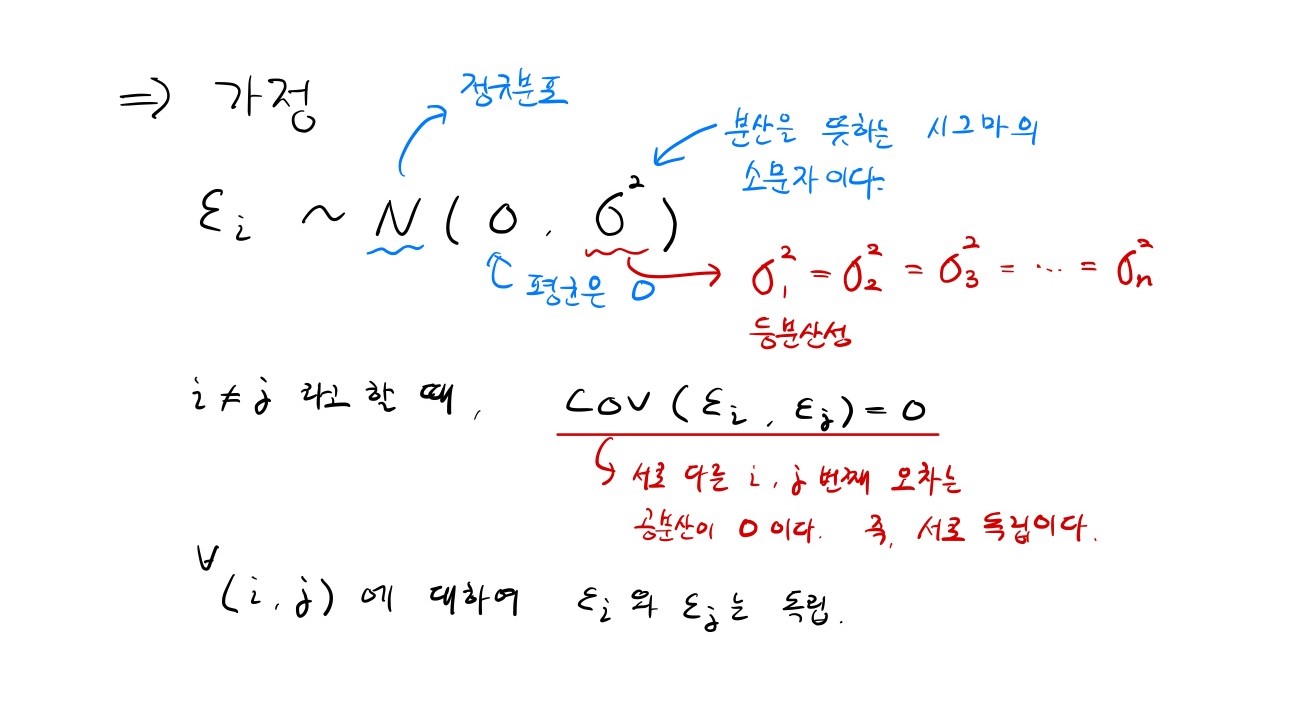
(1) 정규성 : εi는 정규분포를 따른다.(종속성)
(2) 평균은 0 : E(εi) = 0
(3) 등분산성 : var(εi) = 일정한 값
(4) 독립성 : εi들은 서로 독립이다. (i 번째 ε)
(5) 독립변수 x는 확률 변수가 아니다.
[가정] - 악필이라 죄송합니다.
 |
728x90
반응형
'통계 > 회귀분석 - R 프로그래밍' 카테고리의 다른 글
| 적합 회귀선의 특징 (0) | 2021.06.19 |
|---|---|
| 최소 제곱법 설명 및 증명(추정) (0) | 2021.06.19 |
| 단순 회귀 모형 - 최소 제곱법(최소 자승법) (0) | 2021.06.19 |
| 단순 회귀 모형 - 회귀 직선의 추정식과 잔차(error) (1) | 2021.06.19 |
| 회귀 분석 - 단순 선형 회귀(상관계수r) (0) | 2021.06.16 |