· β1 가설검정
가설 - 귀무가설 : β1 = 0 vs 대립가설 : β1 ≠ 0 (거의 대부분 양쪽 검정을 실시한다.)
해석 -
회귀직선의 기울기가 0이다 vs 기울기는 0이 아니다.
회귀의 의미가 없다. vs 의미가 있다.
설명변수와 반응변수는 직선의 관계를 갖지 않는다. vs 직선의 관계를 갖는다.
회귀분석은 타당하지 않다. vs 타당하다.
검정통계량
 |
· β0 가설검정
y의 절편 β0이 0인지를 검정하는 방법도 오차항의 분산 σ**2이 미지이면 기울기 검정과 똑같은 t - 검정을 실시한다.
가설
귀무가설 : β0 = 0 vs 대립가설 : β0 ≠ 0
해석
절편의 값은 0을 지나 간다. vs 절편은 0을 지나지 않는다.
검정 통계량
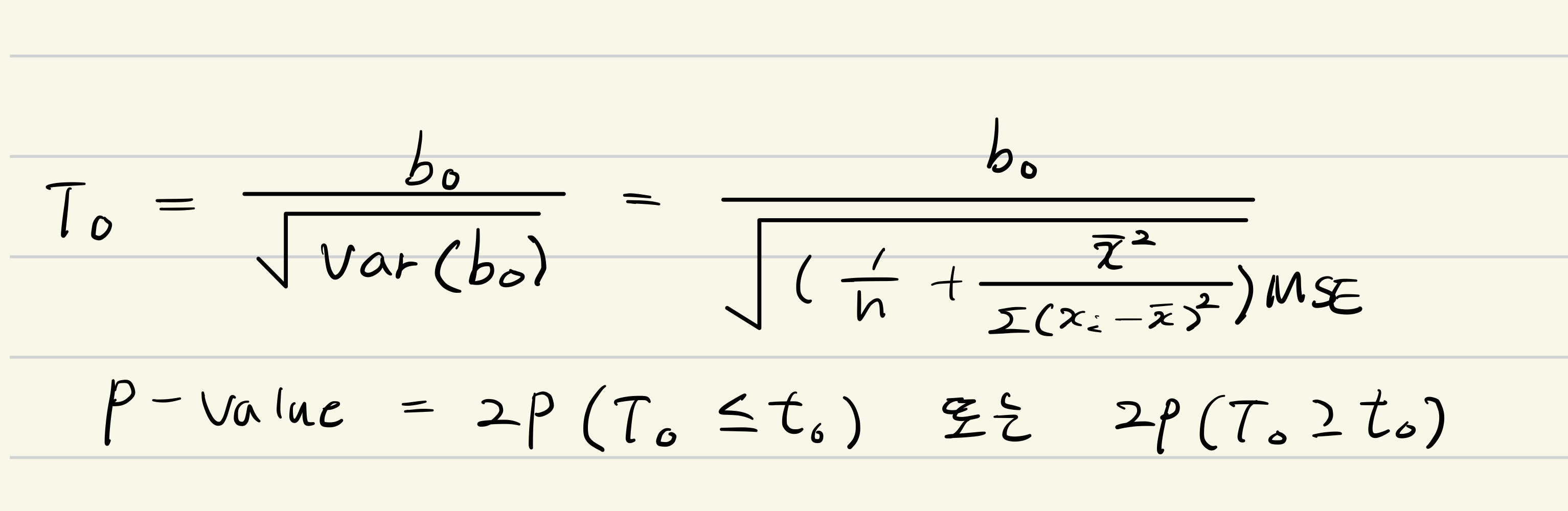 |
· 참고
 |
· y - 절편이 0일수도 있는 경우 회귀식을 찾는 절차
(1) 설명 변수와 반응 변수의 성질을 고려해서 자료의 특성상 원점을 지나는 것이 더 자연스러운 경우
(2) y - 절편이 '0'인지 분명하지 않을 때는 절편이 있는 경우와 없는 경우의 회귀를 모두 실시한 후 MSE의 대소(크기) 비교 한다. 이 때 더 작은 MSE를 갖는 모형을 선택 한다.
=> 왜냐하면 MSE가 작다는 것은 자료가 회귀식에 더 잘 부합하다는 하나의 지표이기 때문이다. (분산의 식을 확인 해보면 된다.)
(3) 2번의 경우에서도 적합의 정도를 가리기 어렵다면, 다시 말해서 절편이 진짜 '0'이라는 확신이 없다면 y - 절편항을 그대로 남겨 두는 것이 좋다. 이 값은 반응 변수의 "기본값"(설명 변수가 0일 때 반응 변수의 값) 의 역할을 할 수 있기 때문이다.
최종적으로 (0, 0)을 지나는 회귀 직선식을 채택한다면 원점을 지나는 회귀를 한다.

'통계 > 회귀분석 - R 프로그래밍' 카테고리의 다른 글
| 회귀분석 - 분산분석 (2) | 2021.06.21 |
|---|---|
| 평균반응량 E[y] = μ(y, x)의 신뢰구간 (0) | 2021.06.20 |
| 절편(b0)의 신뢰구간 (0) | 2021.06.20 |
| 기울기(b1)의 신뢰구간 (1) | 2021.06.20 |
| 잔차의 성질과 오차항(ε)의 분산 추정 (0) | 2021.06.20 |